Why does x & -x equal to the largest power of 2 that divides x?

I recently read in a book that x & -x equals to the largest power of 2 that divides x. For example, 13 & -13 is 1 (2^0), 24 & -24 is 8 (2^3), 14 & -14 is 2 (2^1). Here & means bitwise AND. May be this is just me, but after reading it, I was not able to understand the reasoning. Obviously, & is a bitwise operator and 2 is the base, so there is a connection. But what is the connection actually?

Representation of Negative Numbers in Binary

We should actually start with how numbers are represented in binary. In binary, we have only two digits; 0 and 1. To represent a number, we break it up into a sum of powers of 2. But each power should occur only once. So 13 is written as 13 = 8 + 4 + 1. If we include all the missing powers, then it will be written as 13 = 1*8 + 1*4 + 0*2 + 1. Now pick out all those 0s and 1s before every power and write them in the decreasing orders of their power. Hence 13 = 1101 in base 2. I agree, this is a terrible explanation, but if you contrast with how we represent in base 10, that is, decimal, then it should make sense. For example, 13 = 1*10 + 3*1. Or better, prefer Binary number - Wikipedia. Remember that 2^0 = 10^0 = 1.

Coming back to negative numbers, we have two ways to represent them, one’s complement and two’s complement. Let us assume that all our numbers are going to represented in size of 6 bits. So 13 = 001 101 (space for readability).

Generally, for negative numbers, you reserve the first bit for sign. So, if the first bit is 0, it means the number is positive, else, if it is 1, then the number is negative. Effectively, by this reservation, you are left with only five bits for the magnitude of the number, so we can only represent numbers from -32 to +31 (inclusive).

One’s Complement

In one’s complement, to store a negative number, you invert all the bits in the positive representation of the number.

Take -13. With six bits, binary-form of 13 is 001 101. Inverting the bits gives 110 010.

Two’s Complement

In two’s complement, we invert all the bits of the number and then add 1.

So for 13, inverting all the bits gives 110 010. Now add 1 to it. Therefore -13 in two’s complement is 110 011.

Or in other words, we find the one’s complement and add 1 to it.

Coming back to our original concern, x & -x gives you the largest power of 2 that divides x only when -x is represented in two’s complement.

Thankfully, two’s complement is the most used format, at least in computers, as per Signed number representations - Wikipedia.

There is no definitive criterion by which any of the representations is universally superior. For integers, the representation used in most current computing devices is two’s complement, although the Unisys ClearPath Dorado series mainframes use ones’ complement.

Largest Power of 2

We have a nice mathemagical property involving the largest power of b in base b format.

In decimal, if a number is followed by k zeroes, then it is divisible by 10^k. For example, 1305200 is divisible by 100, that is, 10^2.

The same happens in binary too. 110 000 (48) is divisible by 10 000 (16), that is, 2^4.

Decoding x & -x

Having understood the above sections (you did right 😿?), we can now decode x & -x.

From the previous section, we can say x & -x gives you a number y whose binary representation ends with k number of consecutive zeroes such that y = 2^k divides x.

Now we can rephrase our question as why does x & -x give you a number whose binary representation ends with k number of consecutive zeroes?

Or more directly, we can say, x ends with k number of consecutive zeroes. So we need to do some operation, which can give us a number whose binary form is 100...{k number of zeroes}.

The above statement is our ultimate clue and -x is the crux of the operation.

Say x ends with k zeroes. This means in binary, the number is like the following.

x = VARIABLE_PART 1 CONSTANT_PART

Here VARIABLE_PART means a stream of 0s and 1s, we don’t care about actually. CONSTANT_PART is a group of k number of zeroes. ¹

Now take -x. Remember how -x in two’s complement is equal to one’s complement of x plus 1?

-x = INVERT(VARIABLE_PART) INVERT(1) INVERT(CONSTANT_PART) + 1

Ignore INVERT(VARIABLE_PART). It can be anything and is none of our concern. But look at INVERT(CONSTANT_PART). We know CONSTANT_PART is a collection of k zeroes. So what happens when you invert them? They become a collection of k ones!

Okay, so what happens when you add 1 to a collection of k ones? You will get a number whose binary form has 1 followed by k zeroes.

 111...k 1s...111 
 +              1
-----------------
1000...k 0s...000

But in our case, as we have INVERT(VARIABLE_PART) INVERT(1) as the prefix, the carry 1 generated by adding 1 to a k number of ones, will be added to INVERT(1).

INVERT(1) is 0, so 0 + 1 equals 1. Effectively this means, -x is like the following.

-x =
     INVERT(VARIABLE_PART) INVERT(1) INVERT(CONSTANT_PART) 
     +                                                   1
     -----------------------------------------------------
   = INVERT(VARIABLE_PART) INVERT(1) 111111...k 1s...11111
     +                                                   1
     -----------------------------------------------------
   = INVERT(VARIABLE_PART) INVERT(1) 000000...k 0s...00000
     +                            1 (from carry)
     -----------------------------------------------------
   = INVERT(VARIABLE_PART)        0  000000...k 0s...00000
     +                            1 (from carry)
     -----------------------------------------------------
   = INVERT(VARIABLE_PART)        1  000000...k 0s...00000

Phew that was quite long (at least to type out). Now we just need to bitwise AND the result with x. So x & -x is like the following.

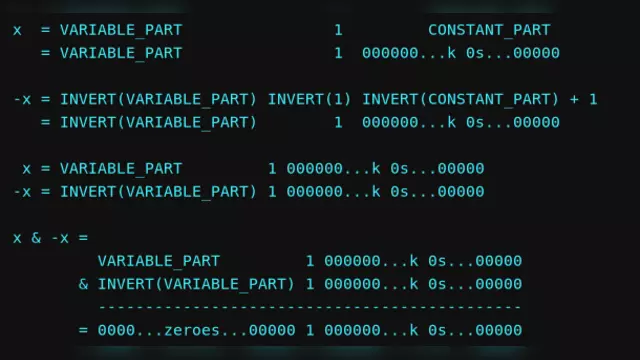
x  = VARIABLE_PART                1         CONSTANT_PART
   = VARIABLE_PART                1  000000...k 0s...00000

-x = INVERT(VARIABLE_PART) INVERT(1) INVERT(CONSTANT_PART) + 1 
   = INVERT(VARIABLE_PART)        1  000000...k 0s...00000

 x = VARIABLE_PART         1 000000...k 0s...00000
-x = INVERT(VARIABLE_PART) 1 000000...k 0s...00000

x & -x =
         VARIABLE_PART         1 000000...k 0s...00000
       & INVERT(VARIABLE_PART) 1 000000...k 0s...00000
         ---------------------------------------------
       = 0000...zeroes...00000 1 000000...k 0s...00000

Observe how VARIABLE_PART & INVERT(VARIABLE_PART) neatly cancels to a bunch of zeroes. The remaining number we have got is a 1 followed by k number of zeroes. That is, we got 2^k 😎.

Conclusion

There are numerous numeric properties we take for granted but there are a few which are like wait, what?!. I don’t know about you, but when I first read about x & -x, my brain went through an infinite loop, wondering why. I was able to understand the reasoning only after thinking about how two’s complement forms the base of logic.

Do you know that two’s complement of x equals 2^N - x, where N is the number of bits for storage? Can you guess why 2^N - x equals one’s complement plus 1?

Hope you enjoyed reading. Please let me know of your thoughts and my mistakes via the links in the footer. Sorry if I went a bit off.

Notes